Què és el sistema binari?
El sistema binari és un sistema de numeració en què els nombres es representen usant tan sols dues xifres: zero (0) i u (1). És el sistema natural de comptatge usat pels ordinadors, ja que internament treballen amb dos nivells de voltatge: encès (o amb presència de càrrega elèctrica, equivalent a 1) i apagat (o sense prèsencia de càrrega elèctrica, equivalent a 0).
Breu introducció histórica
La primera descripció que es coneix d’un sistema binari es remunta al segle III abans de la nostra era, quan el matemàtic indi Pingala va descobrir el concepte del número zero. Es poden trobar, per exemple, usos posteriors del sistema binari en textes clàssics de l’antiga China o en alguns tractats de Sir Francis Bacon (un dels pares de l’actual ciència) en què parlava de fer ús del sistema binari per codificar l’alfabet.
El sistema binari modern va ser documentat en la seva totalitat per Leibniz al segle XVII, en el seu article “Explication de l’Arithmétique Binaire”. En aquest, Leibniz ja va usar el 0 i l’1, com en el sistema de numeració binari actual.
No va ser però fins a l’any 1854 que el sistema binari va obtenir la notorietat que posseeix actualment: el matemàtic britànic George Boole va publicar un article detallant un sistema de lógica (que acabaria anomenant-se Àlgebra de Boole) sustentat sobre la teoria del sistema binari. L’Àlgebra de Boole va esdevenir un factor fonamental per al desenvolupament dels sistemes electrònics actuals.
Representació d’un nombre decimal en sistema binari
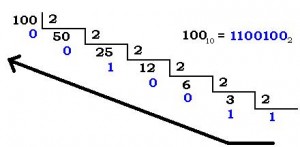
Es divideix el nombre en sistema decimal entre 2. El resultat d’aquesta divisió es torna a dividir entre 2, i així successivament fins que el dividend sigui menor que el divisor (2). És a dir, quan el número a dividir sigui 1 es finalitza la divisió.
Seguidament, s’ordenen els residus de les divisions des de l’últim fins al primer (es coloquen en ordre invers a com a apareixen a les divisions). Aquest serà el número binari resultant de la conversió.
Conversió d’un nombre decimal a binari.
Comptatge en sistema binari amb els dits de la mà
Per tal de realitzar el comptatge en sistema binari mitjançant els dits de la mà cal que coneguem inicialment algunes característiques més del sistema binari:
- En funció del nombre de dígits que usem per representar els nostres nombres en binari podrem representar més o menys nombres decimals. Així, per exemple, si només fem servir un dígit per a la representació en binari, tan sols podrem representar dos nombres decimals: el 0 i l’1. Si fem servir dos dígits per al nostre sistema binari podrem representar quatre nombres decimals: 0, 1, 2 i 3. Si fem servir tres dígits, podrem representar vuit nombres decimals: 0, 1, 2, 3, 4, 5, 6 i 7. I així successivament. La relació diu que essent n el nombre de dígits binaris a usar, podrem representar els nombres decimals fins a 2n – 1 (incloent el 0).
- Els dígits d’un nombre en sistema binari (en el món de la informàtica) també són coneguts com a bits.
- A cada bit d’un nombre en sistema binari se li assigna un pes en funció de la seva posició. Així el dígit de més a la dreta és el dígit de més pes i el dígit de més a l’esquerra és el dígit de menor pes.
- El pes dels dígits indica el valor que un determinat dígit aporta al càlcul del seu equivalent decimal quan es troba actiu. Sempre comencem a comptar des del bit de menys pes cap al de més pes. Així, el bit de menys pes (el de més a l’esquerra) aporta un valor 0 si no està actiu i un valor 20 si està actiu (1). El segon bit de menys pes aporta un valor 0 si no està actiu i un valor 21 si està actiu (2). El tercer bit de menys pes aporta un valor 0 si no està actiu i un valor 22 si està actiu (4). I així anar fent. La norma general diu que donat un bit en la posició n, la seva aportació és de 2n-1 quan està actiu, i de 0 en cas contrari.
Sabent això, ja estem preparats per apendre a comptar en binari amb les nostres mans!
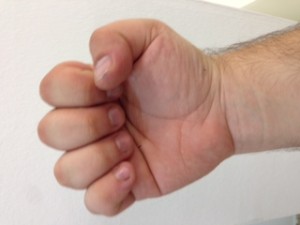
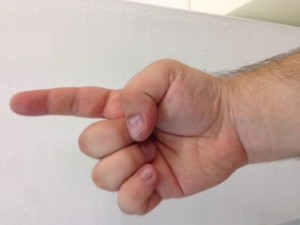
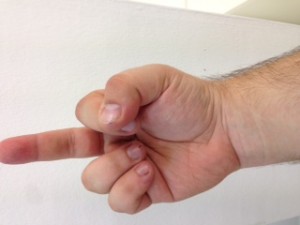
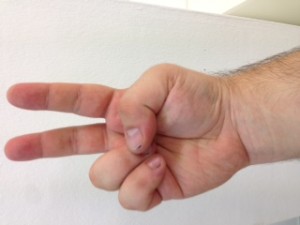
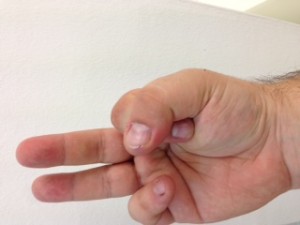
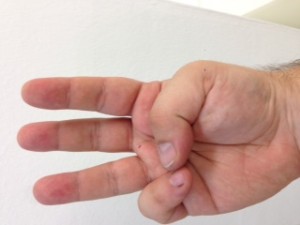
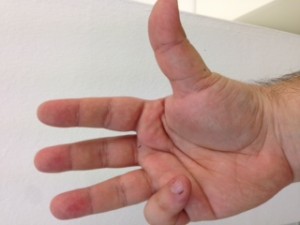
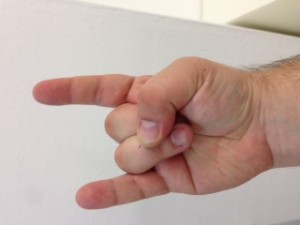
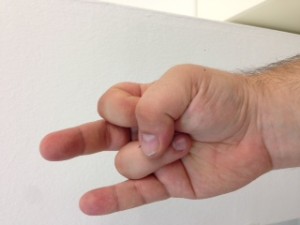
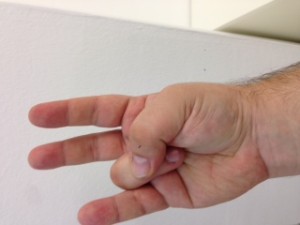
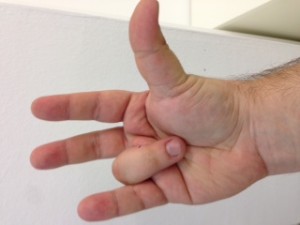
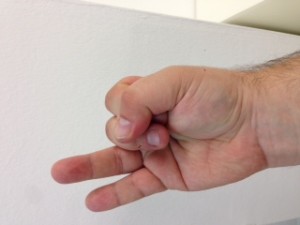
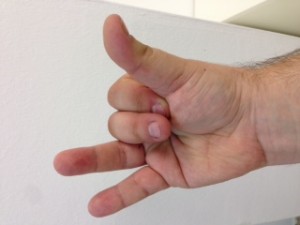
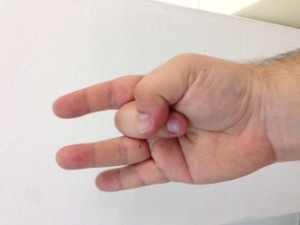
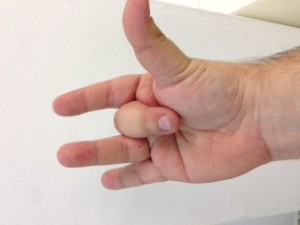
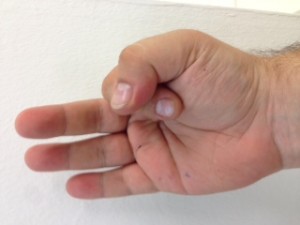
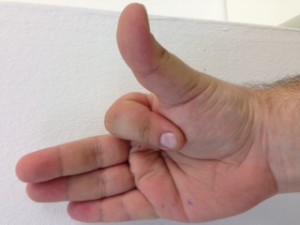
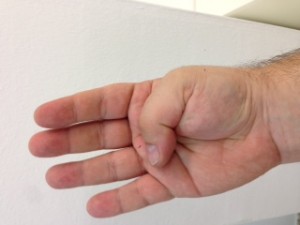
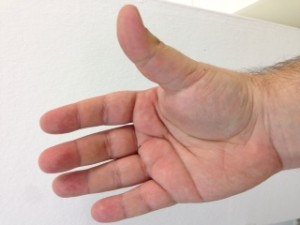
El procés consisteix en aixecar la mà dreta i posar-la amb el puny tancat mirant cap a nosaltres. Vista així, la nostra mà consta de cinc bits, on el bit de menys pes pertoca al dit gran, i el de més pes al dit petit. Direm que un bit està actiu si el dit corresponent es troba aixecat. Direm que un bit està inactiu si el dit corresponent es troba plegat. Quants nombres decimals podem representar mitjançant una mà? Segons el que hem explicat anteriorment, si disposem de 5 dígits podem representar els decimals fins a 25 – 1, és a dir, (2 x 2 x 2 x 2 x 2) – 1 = 32 – 1 = 31 nombres decimals i el 0 (que és l’absència de representació).
No us ho creieu? Mireu doncs!
| Nombre Decimal | Nombre Binari | Nombre Manual |
|---|---|---|
| 0 | 00000 |  |
| 1 | 00001 |  |
| 2 | 00010 |  |
| 3 | 00011 |  |
| 4 | 00100 |  |
| 5 | 00101 |  |
| 6 | 00110 |  |
| 7 | 00111 |  |
| 8 | 01000 |  |
| 9 | 01001 |  |
| 10 | 01010 |  |
| 11 | 01011 |  |
| 12 | 01100 |  |
| 13 | 01101 |  |
| 14 | 01110 |  |
| 15 | 01111 |  |
| 16 | 10000 |  |
| 17 | 10001 |  |
| 18 | 10010 |  |
| 19 | 10011 |  |
| 20 | 10100 |  |
| 21 | 10101 |  |
| 22 | 10110 |  |
| 23 | 10111 |  |
| 24 | 11000 |  |
| 25 | 11001 |  |
| 26 | 11010 |  |
| 27 | 11011 |  |
| 28 | 11100 |  |
| 29 | 11101 |  |
| 30 | 11110 |  |
| 31 | 11111 |  |
I això amb una sola mà! Què me’n dieu de fer servir les dues mans? Us ho creieu si us diem que es pot comptar fins a 1023? Proveu-ho! El poder és a les vostres mans!